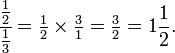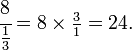Dalam matematik, perpuluhan berulang 0.999…, yang juga ditulis sebagai  atau
atau  , menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.
, menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.
 atau
atau  , menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.
, menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.Beberapa abad yang lalu, para penyelidik dalam bidang pembelajaran matematik telah mengkaji penerimaan persamaan ini di antara para pelajar. Sebilangan besar telah menolak atau membantah persamaan tersebut, pada peringkat awalnya. Kebanyakan daripada mereka terpesong akibat buku-buku teks, para guru dan penaakulan aritmetik seperti di bawah untuk menerima bahawa kedua-dua daripada persamaan ini adalah serupa. Walaubagaimanapun, mereka seringkali tidak disenangi, seterusnya mempelawa hujah-hujah yang lebih mendalam lagi. Pertimbangan para pelajar dalam menolak atau menerima persamaan ini adalah secara umumnya berdasarkan salah satu daripada intuisi terhadap nombor-nombor benar yang silap; sebagai contoh, bahawa setiap nombor benar mempunyai sebuah perkembangan perpuluhan yang unik, serta infinitesimal (perpuluhan tidak terhad) bukan sifar seharusnya wujud, ataupun bahawa perkembangan persamaan 0.999… akhirnya menemui jalan mati. Sistem-sistem bernombor yang memikul intuisi-intuisi ini boleh dibina, namun berada di luar sistem bertaraf umum nombor benar yang digunakan dalam matematik tahap rendah, dan juga tahap tinggi. Memang benar, sesetengah mengandungi nombor-nombor yang "pantang" bernombor 1; selalunya ini tidak berkaian dengan 0.999…, namun dianggap sesuatu yang cukup menarik dalam analisis matematik.
Ketidak-unikan akan perkembangan benar seperti 0.999… tidak terhad kepada sistem perpuluhan sahaja. Kejadian yang serupa berlaku dalam integer base selain daripada nombor 10, dan ahli matematik juga telah menyatakan kaedah untuk menulis nombor 1 dalam base bukan integer. Namun kejadian ini bukannya tertakluk kepada 1 sahaja: setiap nombor perpuluhan bukan sifar memiliki satu kembar dengan nombor-nombor 9 yang mengikutnya. Di atas sebab-sebab kemudahan, perpuluhan tersebut seringkali menjadi wakil yang digemari, seterusnya menyumbang kepada kesalahan konsep yang mengatakan bahawa ia adalah satu-satunya wakil yang wujud. Namun sebenarnya, apabila perkembangan tidak terhad dibenarkan, setiap sistem posisi bernombor mengandungi satu nombor yang tidak terbatas akan perwakilan alternatif nombor-nombor. Sebagai contoh, 28.3287 merupakan nombor yang sama dengan 28.3286999…, 28.3287000, atau nombor-nombor perwakilan yang lain. Identiti-identiti berbeza ini telah digunakan bagi kemudahan untuk memahami corak dalam perkembangan perpuluhan terhadap pecahan dan struktur ringkas suatu frektal, iaitu Set Kandor. Mereka juga berlaku dalam sebuah penyiasatan klasik tentang kejadian tidak terhad terhadap suatu set nombor-nombor benar.
Link :
http://www.youtube.com/watch?v=Os7zKwY91LY
atau
http://www.youtube.com/watch?v=OCqEXZbt1e0&feature=related

 .
. . Boleh dibayangkan yang setiap kek penuh itu dibahagikan kepada empat bahagian, menjadikan penyebut untuk kek penuh (nombor bulat) sama dengan penyebut kek yang telah dipotong,
. Boleh dibayangkan yang setiap kek penuh itu dibahagikan kepada empat bahagian, menjadikan penyebut untuk kek penuh (nombor bulat) sama dengan penyebut kek yang telah dipotong,  , jadi
, jadi  ialah cara lain untuk menulis nombor bercampur
ialah cara lain untuk menulis nombor bercampur  adalah sama dengan pendaraban dengan satu, dan sebarang nombor yang didarab dengan satu mempunyai nilai yang sama dengan nombor asal. Contohnya, untuk pecahan
adalah sama dengan pendaraban dengan satu, dan sebarang nombor yang didarab dengan satu mempunyai nilai yang sama dengan nombor asal. Contohnya, untuk pecahan  : apabila kedua-dua pengangka dan penyebut didarab dengan 2, hasilnya adalah
: apabila kedua-dua pengangka dan penyebut didarab dengan 2, hasilnya adalah  , yang memiliki nilai yang sama (0.5) dengan
, yang memiliki nilai yang sama (0.5) dengan  ,
,  ,
, 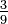 dan
dan  kesemuanya adalah pecahan setara.
kesemuanya adalah pecahan setara.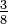 ialah pecahan termudah kerana satu-satunya faktor untuk 3 dan 8 ialah 1.
ialah pecahan termudah kerana satu-satunya faktor untuk 3 dan 8 ialah 1. , ialah
, ialah  .
. (kadang-kadang 1 dirujuk sebagai "penyebut halimunan"). Maka, kecuali untuk sifar, setiap pecahan atau nombor bulat memiliki satu salingan. Salingan untuk 17 ialah
(kadang-kadang 1 dirujuk sebagai "penyebut halimunan"). Maka, kecuali untuk sifar, setiap pecahan atau nombor bulat memiliki satu salingan. Salingan untuk 17 ialah 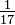 .
. dan
dan  merupakan pecahan kompleks. Untuk memudahkan satu pecahan kompleks, bahagikan pengangka dengan penyebut seperti dalam pecahan yang lain (lihat bahagian pembahagin untuk keterangan lebih lanjut):
merupakan pecahan kompleks. Untuk memudahkan satu pecahan kompleks, bahagikan pengangka dengan penyebut seperti dalam pecahan yang lain (lihat bahagian pembahagin untuk keterangan lebih lanjut):